« Wasan » : les surprenantes découvertes mathématiques d’un Japon replié sur soi

De précieuses tablettes en bois

Les sangaku sont un genre de ema, des tablettes votives en bois que les gens ont l’habitude d’offrir aux temples et sanctuaires lorsqu’ils sont confrontés à une épreuve ou un problème particulier et cherchent une assistance. Ce qui distingue les sangaku des autres ema, c’est que chacun d’entre eux offre une célébration — et une preuve — de la découverte d’une solution nouvelle à un difficile problème lié au wasan, la tradition japonaise des mathématiques élaborée à l’époque d’Edo (1603-1868). De concert avec des documents contemporains, les sangaku constituent des ressources historiques inestimables qui nous permettent de retracer l’évolution du wasan au fil des siècles. On dénombre aujourd’hui au Japon environ un millier de sangaku qui ont survécu à l’épreuve du temps.

Peter Wong, professeur de mathématiques au Bates College dans le Massachusetts, est un spécialiste de la topologie et un chercheur engagé dans le domaine des sangaku. Il s’est rendu au temple Myôjôrin-ji, dans la ville d’Ôgaki, pour observer les sangaku de sa collection. C’était son septième voyage au Japon, et il avait l’intention de consacrer trois semaines à la visite de divers endroits pour examiner les sangaku préservés sur place et rencontrer des chercheurs dans le domaine du wasan.

Wong est loin d’être le seul chercheur non-Japonais à avoir cédé à la fascination pour les sangaku. Trois caractéristiques uniques en leur genre expliquent ce niveau d’intérêt : le haut degré d’accomplissement atteint par le wasan malgré l’isolement dans lequel il se trouvait confiné ; le fait que les sangaku étaient écrits par des gens de toutes sortes d’horizons, dont des femmes et des enfants ; la diversité géographique du phénomène, avec des offrandes de sangaku effectuées aussi bien dans les grandes villes que dans les zones rurales.

Le théorème du hexlet avec un siècle d’avance

Dans le numéro 138 de la prestigieuse revue scientifique Nature, publié en 1936, le chimiste britannique Frederick Soddy a pubié un poème intitulé « Le hexlet ». Ce fut la première apparition de ce qu’on appelerait plus tard le « théorème du hexlet de Soddy », qui décrit certaines relations au sein d’une chaîne de six sphères connectées.

Par souci de précision, qu’on me permette de présenter les détails du théorème ainsi que l’histoire qui se trouve à l’arrière-plan de sa découverte, telle qu’elle est racontée dans Sacred Mathematics : Japanese Temple Geometry (Mathématiques sacrées : géométrie de temple japonaise), un ouvrage co-écrit par Fukagawa Hidetoshi, un chercheur en wasan et ancien professeur de mathématiques dans l’enseignement secondaire titulaire d’un doctorat de l’Académie bulgare des sciences, et le théoricien de la physique Tony Rothman, qui a enseigné à Harvard et dans d’autres établissements d’enseignement supérieur.

Selon le résumé qu’en donnent Fukagawa et Rothman, le théorème s’énonce ainsi : si deux sphères de rayons a et b sont contenues dans une grande sphère de rayon r, tangentes les unes aux autres et à la surface interne de la sphère r, un collier d’exactement six sphères — chacune tangentes à ses voisines les plus proches ainsi qu’aux sphères a, b et r — peut être créé autour du « cou » existant entre les sphères a et b. Et plus encore, si les rayons des sphères du collier sont exprimés sous la forme r₁, ... r₆, alors 1/r₁ + 1/r₄ = 1/r₂ + 1/r₅ = 1/r₃ + 1/r₆.

En tant que chimiste étudiant les liaisons ioniques, Soddy s’intéressait aux « problèmes de contenance » lorsqu’il s’interrogeait sur le nombre de cylindres et de cercles de rayons différents pouvant s’insérer dans de plus grands cercles. Il a également participé avec le physicien Ernest Rutherford, originaire de la Nouvelle-Zélande, à la découverte de la transformation nucléaire due à la désintégration radioactive, et gagné le prix Nobel en 1921 pour ses « recherches sur l’origine et la nature des isotopes ». Tout ceci contribue d’une certaine façon à expliquer pourquoi son nom est resté attaché au théorème du hexlet mentionné plus haut.

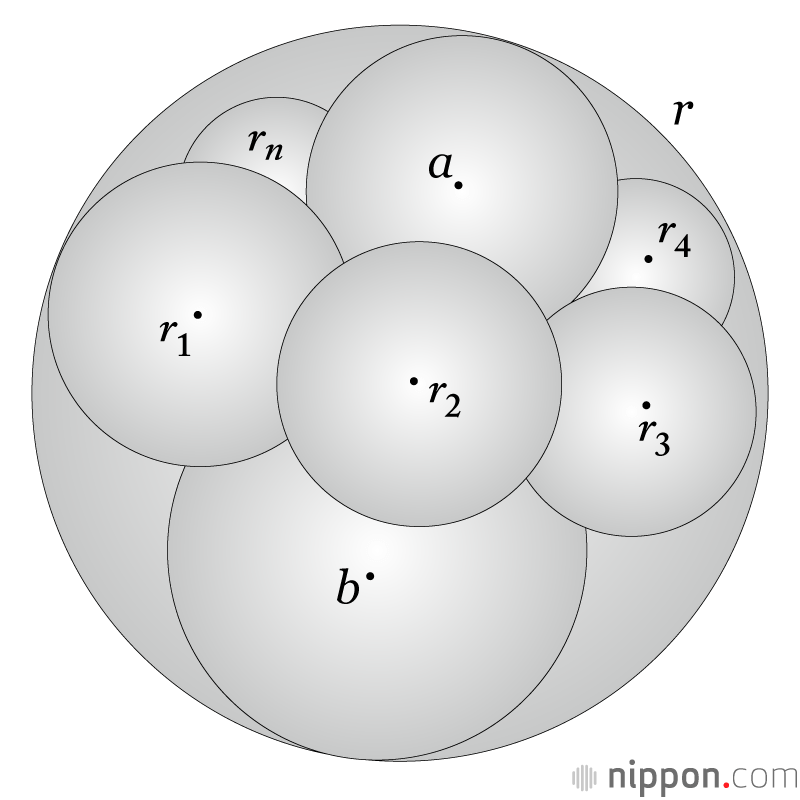
Un collier d’exactement six sphères peut être construit autour du « cou » existant entre les phères a et b. (Image : Nippon.com)

Selon Fukagawa, que sa recherche sur les sangaku a mené d’un bout à l’autre du Japon, un homme répondant au nom de Irisawa Shintarô Hiroatsu a donné en 1822 une plaque attestant exactement les mêmes résultats au sanctuaire Samukawa, dans la province de Sagami (aujourd’hui préfecture de Kanagawa). Irisawa était le descendant de marchands originaires des provinces de Hino et de Ômi. Il tenait une boutique, appelée Hinoya, qui vendait des ingrédients destinés aux préparations de la médecine chinoise traditionnelle, du thé et des tissus, tout en pratiquant le wasan. Le sangaku d’Irisawa a disparu, mais son contenu a été enregistré dans un livre de 1832, intitulé Kokon sankan (les mathématiques, hier et aujourd’hui), du mathématicien wasan Uchida Itsumi. Ce dernier était le professeur d’Irisawa, et Kokon sankan contenait un registre de sangaku offerts par ses étudiants.

Reconstitution du sangaku d’Irisawa basé sur des détails tirés de Kokon sankan, actuellement exposé au sanctuaire Samukawa. (Avec l’aimable autorisation d’Abe Haruki)

Les pages appropriées de la copie numérique de Kokon sankan détenue par la Bibliothèque mathématique du Département de mathématiques de l’Université de Kyoto sont reproduites ci-dessous. L’énoncé du problème commence à la cinquème ligne de texte à partir de la droite, et la solution est donnée tout de suite après.

Archive numérique de Kokon sankan, Bibliothèque mathématique, Département de mathématiques, Université de Kyoto.

Une version anglaise de la traduction du problème en japonais contemporain pourrait donner ceci en français :

« Comme le montre l’illustration, placez deux sphères (“soleil” et “lune”) à l’intérieur d’une plus grand sphère extérieure, de façon à ce qu’elles soient toutes deux en contact avec la surface interne de la sphère extérieure, et puis créez une chaîne de sphères connectées dans l’espace qui reste à l’intérieur de la sphère extérieure. Si les diamètres des sphères extérieure, soleil et lune mesurent respectivement 30, 10 et 6 soleil, et que le diamètre de la sphère marquée kô [en bas à droite du diagramme] mesure 5 soleil, trouvez les diamètres des autres sphères. »

La réponse donne les diamètres des sphères restantes dans l’ordre, en commençant par celles marquées otsu, en haut du diagramme. Après la sixième sphère, la solution se termine par « à la septième sphère, nous revenons au point de départ, ce qui met fin au problème ». Autrement dit la « septième » sphère est en fait à nouveau la première – un parfait hexlet.

On voit donc qu’un théorème conçu et élucidé dans le cadre de la recherche d’un homme couronné par le prix Nobel a en fait été découvert un siècle plus tôt par un marchand japonais. Il serait erroné, semble-t-il, de considérer ce genre de bizarrerie intellectuelle comme le fruit d’un simple passe-temps. Quoi qu’il en soit, c’est l’énergie intellectuelle qui animait les Japonais ordinaires qui a permis l’essor du wasan en tant que discipline théorique.

Un « saint mathématique japonais » bat Leibnitz en ce qui concerne le déterminant

Seki Takakazu est un personnage incontournable dans toute discussion à propos du wasan. De même que Matsuo Bashô est connu comme le haisei (« saint du haiku ») et Sen no Rikyû comme le chasei (« saint du thé »), Seki a reçu le surnom de sansei (« saint des mathématiques ») pour la place monumentale qu’il occupe dans ce domaine. Seki, le plus grand mathématicien que le wasan ait jamais produit, est né dans la classe des samouraï aux environs de l’année 1640 et il est mort en 1708, ce qui fait de lui un contemporain d’Isaac Newton (1642-1727) et de Gottfried Leibnitz (1646-1716), qui ont tout deux contribué à l’essor et à la systématisation du calcul. La position de fonctionnaire des finances du Kôfu han (domaine de Kôfu), occupée pendant des années par Seki, faisait de lui une sorte de mathématicien professionnel.

La longue liste des réalisations de Seki inclut des solutions à bien des problèmes qui se posaient alors au sein du wasan, mais ce qui mérite au premier chef de retenir notre attention est son adoption du concept de déterminant et sa découverte des nombres de Bernoulli. Au cours de sa vie, Seki n’a publié qu’un seul livre, le Hatsubi sanpô (Mathématiques détaillées), mais après sa mort ses disciples ont publié l’ouvrage en quatre volumes Katsuyô sanpô (Recueil de résultats mathématiques importants, 1712) et mis en circulation un grand nombre de manuscrits exposant les résultats auxquels il était parvenu.

Seki répertoriait les problèmes et les équations du wasan en trois catégories, « visible », « obscur » et « caché », dont chacune devait être abordée de la façon adéquate. Les problèmes « visibles » étaient ceux qui relevaient des opérations arithmétiques courantes (addition, soustraction, multiplication et division). Les problèmes « obscurs » étaient ceux qui impliquaient des équations avec une variable inconnue, et les problèmes « cachés » avaient au moins deux variables inconnues. Dans l’approche des problèmes « cachés » propre à Seki figure une combinaison d’opérations qu’il désigne par les termes « interchange » (alternance) et « cross-multiplication » (multiplication croisée) (kôshiki et shajô), qui impliquent effectivement l’extraction d’un déterminant. Seki, dit-on, a divulgué cette méthode en 1683.

Leibnitz, quant à lui, raconte sa rencontre avec l’idée de déterminant dans une lettre adressée en 1693 au mathématicien français Guillaume de l’Hôpital, mais les détails restent obscurs. C’est seulement en 1846 que le mathématicien français Pierre Frédéric Sarrus a fait paraître une méthode permettant de calculer des déterminants de troisième ordre de la même façon que Seki. Ceci étant, on peut voir que l’adoption par Seki du concept de déterminant a précédé d’au moins une dizaine d’années celle de Leibnitz.

Même les gens qui ont jadis eu beaucoup de mal avec les mathématiques et frémissent à l’idée d’une nouvelle rencontre avec les équations simultanées devraient être en mesure de reconnaître le génie de Seki dans l’image ci-dessous. Ces diagrammes proviennent des pages de la copie de Kaifukudai no hô (méthode de résolution des problèmes cachés) détenue par l’Académie japonaise qui expliquent l'« alternance » et la « multiplication croisée ». Le processus est exactement identique à la « méthode Sarrus » enseignée dans les manuels de mathématiques contemporains.

Méthodes d’extraction d’un déterminant

Loin de moi l’idée de restreindre exclusivement la discussion aux questions de priorité, mais examinons néanmoins un autre exemple de « l’arrivée en premier » de Seki : les nombres dits de Bernoulli. On peut les voir comme une suite de nombres spéciaux utilisés pour trouver les résutats d’additions telles que 1 + 2 + 3 + . . . , 1² + 2² + 3² + . . . ,1³ + 2³ +3³ + . . . , et 1^k + 2^K + 3^k + . . . en général.

Non seulement les nombres de Bernoulli restent en usage aujourd’hui dans de tels calculs, mais on s’est aperçu entre-temps qu’ils entretiennent des liens avec bien d’autres domaines des mathématiques. Le nom de « nombres de Bernoulli » leur a été attribué parce qu’ils ont indéniablement été élucidés pour la première fois par le mathématicien suisse Jakob Bernoulli dans un ouvrage de 1713 intitulé Ars Conjectandi.

La découverte par Seki des suites de nombres rapportée dans Katsuyô sanpô figure dans une section de l’ouvrage intitulée « Daseki jutsu », ou « Technique pour trouver des sommes de pouvoirs ». Or cet ouvrage a été publié en 1712 – un an avant Ars Conjectandi.

Du vivant de Seki, les politiques de contrôle strict des frontières mises en œuvre par le shogunat d’Edo interdisaient pratiquement toute communication avec le monde extérieur. Il n’en est pas moins clair que Seki et Bernoulli sont parvenus à la vérité en employant la même méthode.

« Daseki jutsu » dans Katsuyô sanpô (avec l’aimable autorisation des Archives numériques de la Bibliothèque de la Diète nationale) à côté de Ars Conjectandi (avec l’aimable autorisation des Archives Internet).

Résoudre des équations d’ordre plus élevé

Seki et ses successeurs ont à leur actif la découverte de bien d’autres vérités mathématiques que celles décrites ci-dessus, vérités découvertes tantôt avant les mathématiciens européens et tantôt après. Pour n’en nommer que quelques unes, on peut citer le théorème de Descartes, les cercles de Malfatti, la série de Taylor, des calculs de plus en plus précis de la valeur de Pi, des solutions approximatives d’équations d’ordre plus élevé. La valeur de Pi calculée par Takebe Katahiro, disciple estimé de Seki, comporte 41 décimales, et l’on dit qu’un mathématicien wasan a cherché une solution approximative à une équation du 1,458^e degré. Tous ces résultats ont été obtenus grâce à l’usage des sangi et du sanban, les « bâtons de calcul » et la « feuille de calcul » sur laquelle ils sont disposés, de façon à créer une sorte de proto-ordinateur utilisé manuellement par les mathématiciens wasan.

Des sangi longs de 8 à 13 centimètres étaient disposés dans les cases d’un sanban pour représenter des nombres. Cette image montre le nombre « 19 376 ». (Avec l’aimable autorisation de Fukagawa Hidetoshi)

Au Japon, l’idée erronée selon laquelle le wasan ne dépasserait pas le niveau de l’arithmétique enseignée à l’école primaire continue de prévaloire, et la liste que je donne ci-dessus des « découvertes d’envergure mondiale » vise en partie à battre en brèche ce préjugé. Mais s’il est une chose dont j’aimerais que la connaissance se répande, c’est bien le fait que, même pendant les années d’isolement de leur pays, les Japonais prenaient plaisir à faire avancer les mathématiques.

Laissons le dernier mot au professeur Wong, que nous avons rencontré dans les premiers paragraphes de cet article. Wong est d’origine chinoise, et il a formulé un commentaire sur l’essor du wasan qui a laissé une forte impression :

« Regardez la Chine et d’autres pays asiatiques. Le Japon est le seul endroit du monde dont la population a échappé à la guerre pendant 260 ans. Le peuple japonais a eu la bonne fortune d’être en mesure de se concentrer sur les activités culturelles plutôt que guerrières. »

Ce sangaku donné au sanctuaire Isobe de Sabae, Fukui, pose la question de la quantité de sake consommée par les participants à la fête de la contemplation des fleurs. (Avec l’aimable autorisation du sanctuaire Isobe)

(Photo de titre : le professeur Peter Wong en train d’examiner le sangaku du Myôjôrin-ji. © Abe Haruki)