Edo-Period Teens Tackling Math’s Toughest Problems: A Historical Look at Japan’s “Wasan” Math

Related article › Japan’s “Wasan” Mathematical Tradition: Surprising Discoveries in an Age of Seclusion

In the late Edo period (1603–1868), a sangaku was donated to the temple Myōjōrinji in the city of Ōgaki, Gifu, that still survives today. This is a subset of the ema, wooden plaques presented by parishioners hoping to overcome some hardship in life, but sangaku have a narrower focus, commemorating a new solution to a problem in Japan’s Edo-period (1603–1868) wasan tradition of mathematics. The list of contributors to this sangaku includes two female names, and another contributor was a teenage boy—valuable evidence that wasan was practiced not only by adult men but also by women and children.

The sangaku at Myōjōrinji. (Courtesy of Fukagawa Hidetoshi)

The Teens on Myōjōrinji’s Sangaku

Myōjōrinji’s sangaku was donated in 1865 by “Asano Genjūrō, student of Asano Takamitsu, and others.” The third problem on the sangaku is attributed to “Kawai Sawa,” a female name. Kawai was 16 at the time. Fukagawa Hidetoshi, a wasan researcher and former high school mathematics teacher who received his PhD from the Bulgarian Academy of Sciences, explains the problem and its solution as follows.

Detail of the Myōjōrinji sangaku, showing the problem solved by Kawai Sawa et al. (Courtesy of Fukagawa Hidetoshi)

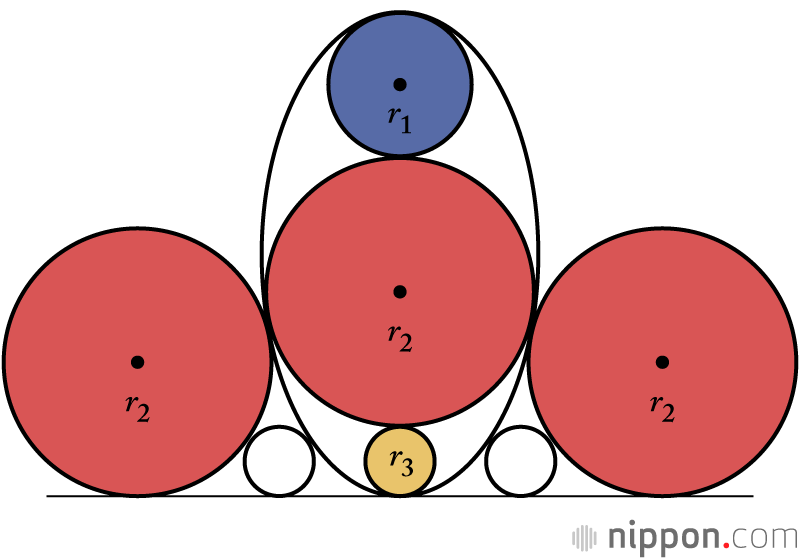
The mathematical problem solved by Kawai Sawa.

An ellipse containing red, blue, and yellow circles with three different radii sits on a straight line as shown. Each of these three circles touche the edge of the ellipse. Red and white circles touch the ellipse from left and right, with the ellipse in the middle. How do you find the diameter of the yellow circle when the blue circle is enlarged to its maximum size? Solution: Use an abacus to divide the diameter of the blue circle by 3.

“In the sangaku diagram, the additional circle at the top of the ellipse disappears when a proper ellipse is drawn and the blue circle is maximized, so it’s better not to include it. Still, according to the text of the problem, the answer is correct,” explains Fukagawa. “This problem is at or above the level expected of an undergraduate math major, and it’s startling to learn that a sixteen-year-old girl was studying such difficult problems.”

What’s more, on the same sangaku, the sixth problem from the right is attributed to “Okuda Tsu,” another female name (age not recorded), while the tenth problem is attributed to a 15-year-old boy named Tanabe Suteji Shigetoshi. Unfortunately, we know nothing else about these people, but their appearance here does prove that women and children worked on wasan problems alongside adult men—and that their abilities were respected enough to record them on these plaques.

Women in the Mathematical Company of Samurai

Nor was this phenomenon peculiar to Ōgaki. The sangaku below was donated to Sōzume Hachimangū shrine in the modern-day city of Okayama in 1861 by the students of a local wasan school. According to Fukagawa, the central figure in the picture is the school’s teacher, while the rest of the people are students, some using abacuses and others using sangi and sanban (calculating sticks and mats) to solve higher-order equations. Among the students are two women and a boy looking at abacuses. (The samurai blowing his nose at bottom left is another charming detail.)

The sangaku at Sōzume Hachimangū shrine. (Courtesy of Fukagawa Hidetoshi)

To the left and right of the central standing screen are the following three problems:

1. Given a square of area 85,000 square units, find the length of one side.
2. Given a circle inscribed in a triangle with sides of length 10, 17, and 21, find its diameter.
3. Given a cube of volume 1,881,676,371,789,154,860,897,069, find the length of one edge.

Modern solutions of these using calculators or computers would be as follows:

1. x² － 85,000 = 0.
   Answer: 291.547 . . .
2. Calculate the triangle’s area S using Heron’s formula,* then calculate the circle’s radius r using: r = 2S/(a + b + c).
   Answer: 2r = 7.
3. x³ － 1,881,676,371,789,154,860,897,069 = 0.
   Answer: 123,456,789.

* “Heron’s formula,” mentioned in the second problem, is a way of obtaining a triangle’s area S when only the lengths of its sides (a, b, and c) are known. The formula is commonly written: S = √(s(s - a)(s - b)(s - c) ), where s = (a + b + c)/2. It is usually learned in high school today, but wasan mathematicians were already familiar with it.

This sangaku is invaluable for the story it tells about women and children mingling with samurai as they worked on mathematical problems, using Heron’s formula, the abacus, and sangi to solve higher-order equations involving numbers with many digits.

Edited by a Doctor’s Daughter?

The title Sanpō shōjo (Arithmetic Girl) has made a number of appearances in the contemporary era—as the name of a 1973 book by Endō Hiroko, rereleased in 2006, followed by a manga version issued starting in 2010. The original text, though, was a three-volume wasan text published in 1775—that is, almost 250 years ago, in the middle of the Edo period. The book was attributed to one Kochū no Inja (“Recluse in a Pot”), described in the book’s preface as “a doctor from Osaka, whose descriptions of mathematical techniques were recorded and edited for publication herein by his daughter Taira Akiko.” Hence, the author explains, the word “girl” (shōjo) in the title.

The book is mentioned in the writings of Aida Yasuaki, a wasan practitioner active at the time, and from this we know that Kochū no Inja’s real name was Chiba Tōzō. Chiba was indeed a doctor from Osaka practicing in Edo, and also a wasan enthusiast who was fully initiated into the Seki school.

Colophon in the third volume of Sanpō shōjo. (Courtesy National Diet Library Digital Archives)

Let’s take a look at the book’s content, drawing on Wasansho sanpō shōjo o yomu (Reading the Wasan Text Arithmetic Girl), by Kotera Hiroshi, a wasan researcher and former teacher at Tōdaiji Gakuen Junior and Senior High School.

Sanpō shōjo begins by introducing a method for calculating pi. The method involves using regular polygons inscribed in a circle: first a square, then an octagon, then a hexadecagon, up to a polygon with the astounding number of more than 100,000 sides. As the text describes, this tells us that circumference ÷ diameter = 355 ÷ 113 = 3.14159202 . . . The book notes, however, that this is still not quite correct, and rather grandly promises to reveal a secret method for expressing pi as an infinite series later.

Calculating pi is used to benchmark supercomputers even today. Its importance to wasan practitioners evidently meant that covering it at the start of the book was necessary to demonstrate the author’s capabilities. The book goes on to cover topics known to modern mathematicians like geometric series, circles inscribed in triangles, quintic equations, least common multiples of fractions, and various combinations of these approaches. The three volumes contain several dozen problems in all, of various types, written in Chinese and Japanese.

Kotera’s close examination of the individual problems found that most of the ones written in Japanese were elementary, while the ones written in Chinese tended to be of intermediate or higher difficulty. The book also includes some mathematical errors, and stands at somewhat of a remove from the wasan mainstream. What kind of girl, then, was the book’s editor, “Akiko”? Unfortunately, apart from this book there is no trace that she even existed. According to Kotera, Aida Yasuaki does not mention her either. Some have suggested that “Akiko” was simply a literary device, but the truth is unknown.

Aida’s evaluation of Sanpō shōjo was generally favorable toward Chiba Tōzō, but Fujita Sadasuke, a rival wasan practitioner of the same generation, was not so generous. He disliked the book so intensely that he wrote a scathing, even emotional attack on it called Sanpō shōjo no hyō (An Evaluation of Arithmetic Girl). The mysterious girl further stoked the flames of a longstanding enmity between the two wasan enthusiasts.

The Further Adventures of Arithmetic Girl

Inspired by this history, Endō Hiroko wrote a novel that breathed new life into Math Girl. Her book, also called Sanpō shōjo, was first published in 1973, with a 2006 reissue. The novel takes its basic cues from the original work, with a young heroine named Aki who is introduced to wasan by her father, a doctor. Aki’s adventures include pointing out an error in a sangaku donated by a proud young samurai who studies at a famous wasan dōjō and opening a school of her own to teach basic arithmetic to impoverished children living in nagaya townhouses. She encounters several historical wasan practitioners along the way.

Endō reportedly went to great lengths preparing to write her novel. She pored over books on the history of mathematics, went to experts for explanations of the finer mathematical points involved, and surveyed the state of mathematics in Japan at the time. This makes the book a fascinating read for those interested in how wasan was regarded and enjoyed by the people of the mid-Edo period. A manga adaptation of the novel, drawn by Akizuki Meguru, was serialized in 2010–14, and an animated movie directed by Tomura Shirō was released in 2015.

The novel Sanpō shōjo (at left; courtesy Chikuma Gakugei Bunko), inspired by the Edo-period wasan text of the same name, and its manga adaptation (courtesy Leed Publishing).

What about the boys of the Edo period? According to Fukagawa’s Reidai de shiru Nihon no sugaku to sangaku (Japanese Mathematics and Sangaku Through Examples), we know from surviving sangaku and related documents that the names of at least 15 boys aged 9 to 15 were recorded on sangaku in Okayama, Kyoto, Shiga, Gifu, Tokyo, Chiba, and Gunma. Most remarkably, Fukagawa notes, they usually appear in connection with what would today be considered college-level problems. Ages were not usually written on sangaku, but Fukagawa believes that intentionally including them was one way adults encouraged young talent.

A German Researcher Discovers Wasan

Dr. Antonia Karaisl, who began researching wasan as an assistant professor at the Waseda Institute for Advanced Study in April 2023, specializes in the history of the relationship between philosophy and science. Her involvement of Japan began when she was exploring the knowledge that the Christian missionaries of the Age of Discovery transmitted along with religion. One of the subjects they taught was Euclidian geometry. Karaisl had hoped to trace how this subject arrived in and spread throughout Japan, but found no sign that it had done so. Mystified, she investigated further, and soon realized that Euclid’s approach had failed to take hold because Japan had already developed a mathematical tradition of its own.

Dr. Antonia Karaisl. (© Abe Haruki)

After reading wasan-related books like Fukagawa and Rothman’s Sacred Mathematics: Japanese Temple Geometry, Karaisl became convinced that wasan and sangaku had developed through a human network that included not just specialists but everyday enthusiasts.

“This kind of human network did not exist in the West,” noted Karaisl. “It included farmers, children, women—and it lasted for 250 years. Can you believe that?”

Karaisl decided to come to Japan to see and study wasan in person. Her proposed research theme, “Japanese sangaku and Euclidean geometry: A history of tangents or parallel lines?” won her an offer to work at WIAS. Her term of residence is three years, and she is spending it busily accumulating sangaku material with explanations in English, in order to share this tradition with researchers around the world. She has met Fukagawa, from whom she received sangaku photographs and related materials. She has also visited Nagasaki, Iwate, and Mie already—and seen the sangaku in Myōjōrinji, of course.

“This work, created by men and women, boys and girls, in their passion for intellectual inquiry, was simply beautiful,” says Karaisl. “I was deeply moved.”

(Originally published in Japanese. Banner photo: Sangaku at Sōzume Hachimangū shrine. Courtesy Fukagawa Hidetoshi.)