La penetración social del ‘wasan’ en el Japón del periodo Edo

Para leer el primer artículo de la serie, clique aquí.

Jóvenes y mujeres en la tablilla del templo de Myōjōrinji

En el templo budista de Myōjōrinji, en la ciudad de Ōgaki (prefectura de Gifu), se ha conservado un sangaku (tablilla votiva que celebra la resolución de problemas matemáticos), ofrendado en los años finales del periodo Edo (1603-1868). Es interesante comprobar que, entre los problemas expuestos, había dos planteados por mujeres y uno por un joven, algo muy significativo, ya que las matemáticas japonesas o wasan no eran cultivadas solo por hombres adultos, sino por un amplio espectro social que abarcaba a ambos sexos y a todas las edades.

Sangaku (tablilla votiva de tema matemático) del templo de Myōjōrinji. (Cortesía de Fukagawa Hidetoshi)

El sangaku del Myōjōrinji fue ofrendado en 1865 por “Asano Genjūrō y otros discípulos de Asano Takamitsu”. La tablilla nos informa de que el tercero de los problemas expuestos había sido planteado por una jovencita de 16 años cuyo nombre era, según se cree, Kawai Sawame. Fukagawa Hidetoshi, un investigador de este tema que, comenzando como profesor de matemáticas en un instituto de bachillerato ha recibido un doctorado de la Academia de las Ciencias de Bulgaria, resume así el planteamiento del problema y su solución.

Detalle del problema matemático resuelto por Sawame recogido en el sangaku que se conserva en el templo de Myōjōrinji.

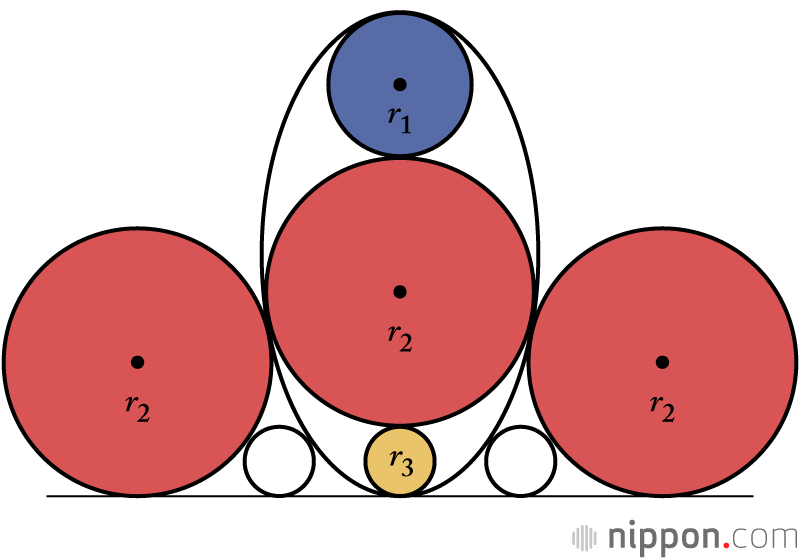
Expresión gráfica del problema resuelto por Kawai Sawame.

Sobre una línea recta se representan un óvalo y varios círculos de cuatro colores: rojo, azul amarillo y blanco. Todos los círculos tocan al contorno del óvalo y, además, los círculos rojos y blancos se sitúan a ambos lados del óvalo tocándose entre sí. La cuestión es cómo hallar el perímetro del círculo amarillo para un perímetro máximo del círculo azul. El esquema de la ilustración se ha hecho a partir de la explicación de Fukagawa. El óvalo representado en el diagrama del sangaku no está trazado con exactitud y por eso se ven diferentes, pero el enunciado del problema en sí es el mismo. La respuesta se halla obteniendo primero el diámetro del círculo azul y dividiéndolo después entre tres, lo cual se hace con ayuda del ábaco.

“El círculo blanco que se ve en la parte superior del diagrama del sangaku desaparece cuando el círculo azul adquiere su diámetro máximo”, explica, “así que es mejor no representarlo, pero en todo caso la respuesta es correcta. Esto corresponde a un nivel de especialización universitaria en matemáticas y es realmente sorprendente que una jovencita de 16 años abordase entonces problemas tan complejos’.

En cuanto a los otros problemas del citado sangaku, el sexto por la derecha es de otra mujer, cuyo nombre era Okuda Tsume, y el décimo de un joven de 15 años llamado Tanabe Suteji Shigetoshi. Desgraciadamente, no sabemos nada sobre sus vidas. Pero lo importante es que junto a hombres adultos encontramos a mujeres y a jóvenes de ambos sexos que abordan problemas matemáticos, los resuelven y dejan su nombre en un sangaku, prueba del reconocimiento obtenido.

Mujeres y samuráis ante una misma ecuación

Y no es solo en el templo de Ōgaki donde comprobamos este fenómeno. El siguiente sangaku, que data de 1861, fue ofrendado al santuario sintoísta de Sōzume Hachimangū, en el actual distrito de Kita de la ciudad de Okayama, por los alumnos de un sanpōjuku (academia de cálculo matemático) local. Según Fukagawa, el personaje sentado en el centro es el maestro, que instruye a sus discípulos mientras estos resuelven ecuaciones de alto grado manejando el ábaco y moviendo las tablillas numéricas sangi sobre el tablero aritmético sanban. Entre los discípulos vemos a dos mujeres con peinado tradicional y a un joven con la vista fija en un ábaco. El detalle cómico lo pone, en la esquina inferior izquierda, el samurái que se suena las narices.

El sangaku del santuario sintoísta de Sōzume Hachimangū. (Cortesía de Fukagawa Hidetoshi).

En la pintura se ve además una mampara y a sus lados estos tres problemas: (1) Hállese el lado de un cuadrado cuya área sea de 85.000; (2) hállese el diámetro de un círculo inscrito en un triángulo cuyos lados tengan una longitud de 10, 17 y 21, y (3) hállese el lado de un cubo cuyo volumen sea 1881676371789154860897069. Expresándolos al estilo de las matemáticas de nuestros días, quedarían así: (1) x²－85000=0, respuesta: 291.5…; (2) el área del triángulo (S) se obtiene mediante la fórmula de Herón, y el radio del círculo (r) sería r=2S/(a+b+c). Respuesta: 2r=7, y (3) x³－1881676371789154860897069=0, respuesta: x=123456789.

La fórmula de Herón utilizada en el problema 2, sirve para obtener el área de un triángulo cuando se conoce la longitud de cada uno de sus lados (a, b, c). Área=√(s(s-a)(s-b)(s-c) ) o semiperímetro=(a+b+c)/2. Los practicantes del wasan conocían esta fórmula, que actualmente suele estudiarse durante el bachillerato.

Es un sangaku muy valioso, ya que expone elocuentemente cómo, al lado de los hombres, muchos jóvenes y mujeres se enfrentaban también a estos problemas y, con la ayuda de la fórmula de Herón, el ábaco y los sistemas de cálculo de la época, resolvían ecuaciones de tercer grado que aplicaban a grandes áreas y a guarismos de muchos dígitos.

El médico y su hija, la “señorita matemática”

A muchos japoneses quizás les suene de haberla visto en alguna novela o en algún cómic, la expresión sanpō shōjo (“señorita matemática” o “señorita calculista”), pero pocos sabrán que tuvo su origen en el título de un libro de wasan publicado en Edo hace ahora cerca de 250 años, en 1775. Su autor, que se presenta con el pseudónimo de Kochū no inja (“ermitaño en la vasija”), dice ser un médico nacido en Osaka y explica que dictó el contenido de los tres tomos que forman el libro a su hija, Taira Akiko, para que lo pusiera por escrito, por lo que ve sobradamente justificado incluir la palabra shōjo en el título.

Gracias a un comentario sobre este libro dejado por uno de los principales matemáticos de la época, Aida Yasuaki, sabemos que el verdadero nombre de su autor era Chiba Tōzō, un médico de Edo oriundo de Osaka que fue también un gran amante del wasan, iniciándose en la escuela Seki, de la que fue transmisor autorizado.

Colofón del tercer y último tomo del libro Sanpō shōjo. (Archivo digital de la Biblioteca Nacional de la Dieta)

Veremos a continuación el contenido del libro, tal como nos lo explica en Wasansho ‘Sanpō shōjo’ wo yomu (“El libro de wasan ‘Sanpō Shōjo’, colección de bolsillo Chikuma Gakugei) otro gran estudioso de esta disciplina, Kotera Hiroshi, que fue profesor de matemáticas del colegio Tōdaiji Gakuen en los niveles de secundaria y bachillerato.

En primer lugar, presenta cómo calcular el número pi. Comienza haciendo aproximaciones al círculo partiendo de polígonos regulares (de ángulos idénticos) circunscritos en él, que van teniendo sucesivamente 4 lados, 8, 16, etcétera, hasta superar los 100.000 lados. Así, obtiene el número pi (3,14159202…) dividiendo 355 (perímetro) entre 113 (diámetro). Pero solo con esto no es suficientemente exacto, por lo que en el colofón del libro nos revela, en tono jactancioso, un método para expresar dicho número mediante una serie matemática (infinita) secreta.

Hoy en día suele usarse la exactitud en el cálculo del número pi como baremo para medir la capacidad de las “supercomputadoras” y también en aquellos tiempos era un asunto importante para los matemáticos japoneses, por eso el Sanpō Shōjo comienza con esta pequeña exhibición de fuerza. Y continúa con explicaciones al estilo japonés contemporáneo y al estilo chino de lo que hoy llamaríamos progresiones geométricas, triángulos con círculos inscritos, ecuaciones de quinto grado, mínimo común múltiplo de fracciones, combinatoria, etc, con varias decenas de problemas.

Tras un detenido análisis de cada uno de los problemas incluidos en el libro, Kotera concluye que los explicados mediante textos propiamente japoneses, más comprensibles, corresponden a un nivel básico o de iniciación, mientras que los escritos al estilo chino clásico serían de nivel intermedio o incluso superior. El libro contiene algunos errores matemáticos y, en general, tiene un carácter muy especial que lo aparta de los manuales de matemáticas convencionales.

¿Cómo cabría imaginar a Akiko, la jovencita que dio forma escrita al libro? Por desgracia, parece ser que no dejó más obra que esta, y el citado Aida tampoco nos dice nada sobre ella. Incluso se sospecha que podría ser una invención. Todo un misterio. Aida acogió con simpatía el libro de Chiba, pero otro matemático contemporáneo, su rival Fujita Sadasuke, llegó a publicar un libro crítico en el que lo descalifica. Vemos, pues, que los dos matemáticos encontraron en la misteriosa señorita una buena excusa para ahondar su rivalidad.

Una atractiva historia llevada al cómic y al anime

La figura histórica de la joven calculista resucitó en el mundo de la ficción de la mano de la escritora Endō Hiroko, que tomó prestado el título del viejo libro de wasan para su novela: Sanpō shōjo. Publicada por primera vez en 1973 por la editorial Iwasaki Shoten, la novela volvió a ser llevada a la imprenta en 2006 por Chikuma Shobō en su colección de bolsillo Gakugei Bunko. En lo básico, la novela respeta la historia real, pues la protagonista es la joven Aki, que es iniciada por su padre médico en la aritmética. Poniendo también en escena a un matemático histórico, la obra narra las peripecias de esta mujer, que osa señalar un error en el problema que un joven y arrogante samurái alumno de una famosa academia acaba de inmortalizar en un sangaku, y dedica su tiempo a enseñar a los niños de los barrios pobres las tablas de multiplicar y los rudimentos del cálculo.

Para escribir su novela, Endō se preparó cuidadosamente y se puso al corriente de todas las circunstancias que rodeaban las matemáticas japonesas de aquellos tiempos, empapándose de la literatura histórica y recabando explicaciones de especialistas en esta ciencia. Este celo documental hace de su novela un texto muy interesante para entender cómo vivían las matemáticas las gentes de mediados del periodo Edo. La novela fue llevada al cómic por el dibujante Akizuki Meguru en 2012 a través de la editorial Leed, y al anime por el director Tomura Shirō y el taller de producción Aka no Joō en 2015.

A la izquierda, portada de la edición de Chikuma Shobo (colección Gakugei Bunko) de la novela Sanpō Shōjo; a la derecha, portada del cómic homónimo (editorial Leed)

Acerquémonos ahora un poco a los jóvenes del sexo masculino. Según explica Fukagawa en su libro Reidai de shiru Nihon no sūgaku to sangaku (“Las matemáticas japonesas y los sangaku vistas a través de los problemas”, editorial Morikita Shuppan), pueden encontrarse los nombres de 15 jóvenes de entre nueve y 15 años en los libros de registros y en los sangaku que se conservan en las prefecturas de Okayama, Kioto, Shiga, Gifu, Tokio, Chiba y Gunma. Llama la atención, continúa Fukagawa, que los problemas que plantean sean en muchos casos de nivel “universitario”. Que sus edades aparezcan en los sangaku, algo poco habitual cuando se trata de adultos, es indicativo de que era una forma de incentivarlos para que desarrollasen su talento, añade el experto.

La admiración de una investigadora alemana

La doctora Antonia Karaisl, profesora alemana del Instituto Waseda de Estudios Avanzados especializada en las relaciones históricas entre filosofía y ciencia, investiga desde abril de 2023 los sangaku. En su primer acercamiento a los temas japoneses, Karaisl indagó en la historia de los primeros misioneros llegados a Japón para tratar de elucidar qué otros contenidos, además de los religiosos, habían transmitido. Se fijó especialmente en la geometría euclidiana, pero no pudo determinar qué grado de penetración alcanzó en Japón debido a la falta de documentación relacionada. Intrigada, indagó en las causas de este hecho y llegó a la conclusión de que estaba relacionado con la existencia y desarrollo en Japón de unas matemáticas propias.

La doctora Antonia Karaisl. (Fotografía del autor del artículo)

Karaisl leyó varios libros sobre el tema, entre ellos Sei naru sūgaku: Sangaku (“Las santas matemáticas: los sangaku”, con versión inglesa en Princeton University Press), escrito conjuntamente por Fukagawa y por el físico estadounidense Tony Rothman. Estas lecturas la convencieron de que el desarrollo del wasan y de los sangaku no se debió solo a un puñado de especialistas, puesto que hay que enmarcarlo en una red de relaciones sociales que se extendía también a las clases populares. Karaisl señala la inexistencia en Europa de una red de relaciones humanas comparable a esta y se admira de su transversalidad, ya que incluía a agricultores, niños y mujeres, y de su duración, pues pervivió durante 250 años.

Con el deseo de llevar a cabo su investigación en contacto directo con los sangaku, Karaisl se decidió a venir a Japón. A ese fin, presentó a un concurso del citado instituto su propuesta “Japanese sangaku and Euclidean geometry: A history of tangents or parallel lines?”, se ganó un puesto como investigadora en el citado instituto que ocupará por tres años, durante los cuales se dedicará a recoger y ordenar toda la información existente sobre los sangaku, traducirla al inglés y contribuir así a que la tradición del wasan sea más y mejor conocida en los círculos académicos internacionales. Para llevar a cabo su empeño, la investigadora está contando con la colaboración de Fukagawa, quien le ha ofrecido fotografías y otros materiales. Ya ha visitado las prefecturas de Nagasaki, Iwate y Mie. El sangaku del templo de Myōjōrinji, por supuesto, lo tiene en su archivo y se declara muy impresionada por la forma en que transmite todo el apasionamiento con el que aquellas mujeres y jóvenes de ambos sexos se enfrentaban a los problemas matemáticos.

Fotografía del encabezado: El sangaku conservado en el santuario sintoísta de Sōzume Hachimangu. (Cortesía de Fukagawa Hidetoshi)

(Traducido al español del original en japonés.)